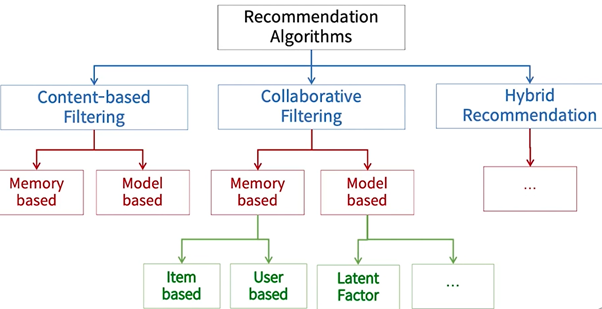
model training 순서
- 데이터 로딩
- 데이터 행, 열 확인
- 데이터 그룹핑 및 집계
- 차트
- 데이터 분할
- 평균 값 계산
- RMSE, MAE 계산
- 포스터 이미지 표시
CBF 기반 예측
아이템 유사도 기반 평점 예측
예) 영화 평점 예상 문제
가정: 유사한 영화에는 유사한 평점을 부여할 것이다.
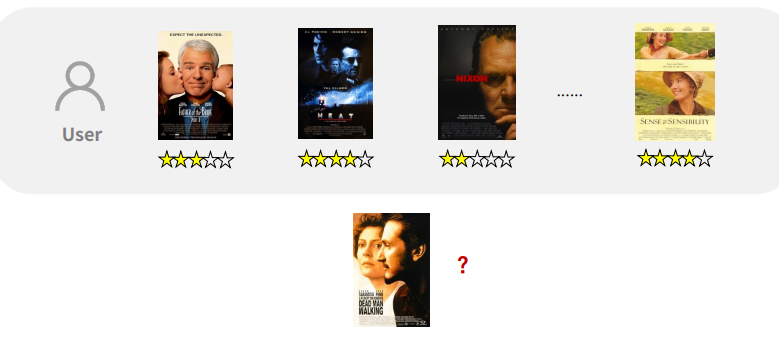
$$ \hat{r}_{u, i} = \frac{\sum _{j \in I_{u}} sim(i, j)*r_{u, j}}{\sum _{j \in I_{u}} sim(i, j)} $$
- r : 사용자 u의 아이템 j에 대한 평점
- I : 사용자 u가 평가한 아이템 집합
- sim(i, j); 두 아이템 i와 j의 유사도
컨텐츠 기반 유사도 측정
sim(i, j)
- 두 아이템 간의 유사도를 어떻게 정량화 할 것이냐가 관건
- CBF에서는 유사도를 정량화 하기 위해서 컨텐츠 자체가 가진 특성을 활용
- 뉴스: 제목, 기사 내용 등
- 영화: 장르, 감독, 출연자, 줄거리 등
- 상품: 카테고리, 가격, 상품 이미지, 상품 설명 등
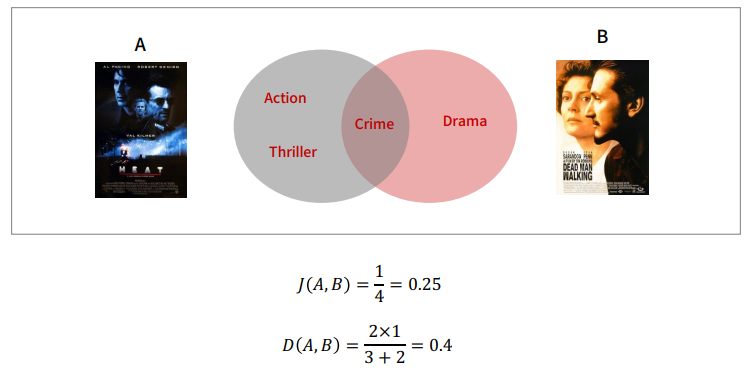
영화의 장르를 이용해 유사도를 측정
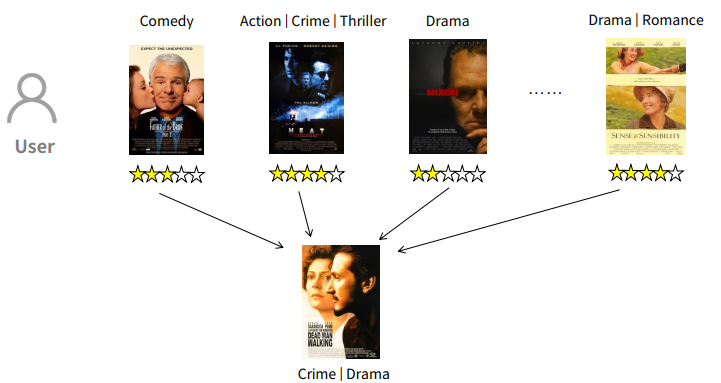
영화를 장르의 집합으로 간주해보면
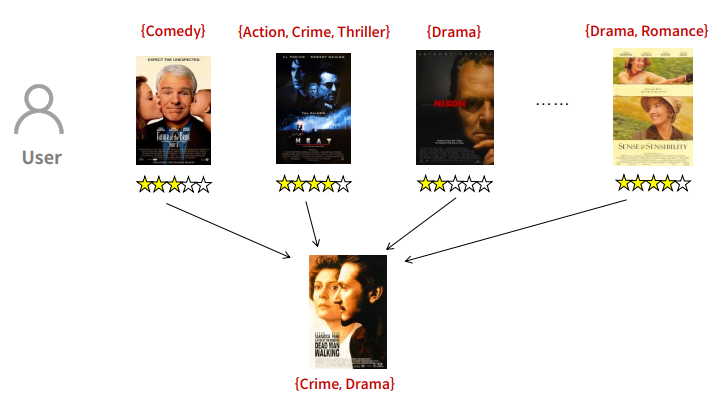
이 때, 집합 유사도에 대해서 알아보자.
1. Jaccard Similarity
$$ sim(i, j) = J(S_{i}, S_{j}) = \frac{|S_{i}\cap S_{j}|}{|S_{i} \cup S_{j}|} $$
2. Sorensen-Dice Similarity
$$ sim(i, j) = D(S_{i}, S_{j}) = \frac{2|S_{i}\bigcap S_{j}|}{|S_{i}| + |S_{j}|} $$
이 때, 집합으로만 계산하면 복잡한 계산을 하기 힘들어 진다.
유사도를 벡터 공간으로 확대
- 원소에 해당하는 차원을 상정하면 집합은 쉽게 벡터로 표현 가능
- 이진 벡터(Binary Vector)는 집합을 표현할 수 있음
- 각 원소(차원)의 가중치를 달리 적용하는 것이 수월해 짐
벡터 연산 중,
Distance & Similarity
1. Euclidean Distance
$$ d(x, y) = ||x - y||_{2} $$
2. (TODO)Cosine Similarity
$$ sim(x, y) = cos(\theta) = \frac{x^{T}y}{||x||_{2}||y||_{2}} $$
3. Pearson (Correlation) similarity
$$ sim(x, y) = P(x, y) = \frac{\sum_{i=1}^{d}(x_{i} - \bar{x}) \cdot (y_{i} - \bar{y})}{\sqrt{{\sum_{i=1}^{d}(x_{i} - \bar{x})^2}} \sqrt{\sum_{i=1}^{d}(y_{i} - \bar{y})^2}} $$
$$ \bar{x} = \frac{1}{d} \sum_{i=1}^{d} x_{i} $$
$$ \bar{y} = \frac{1}{d} \sum_{i=1}^{d} y_{i} $$
TODO) pearson similarity와 cosine similarity의 관계
BoW - 말뭉치
: 하나의 문서 안에 들어간 단어들의 종류와 수

IF-IDF
tfidf(t, d, D) = tf(t, d) * idf(t, D)
TF : Term Frequence
| 방식 | 계산 식 | 설명 |
| 단순 빈도 | f(t, d) | 문서 내에서의 단어의 출현 횟수로 계산 |
| 불린 빈도(boolean) | 1 if t in d, else 0 | 단어의 출현 여부만을 고려 |
| 로그 스케일 빈도 | log(f(t, d) + 1 ) | - 출현 빈도를 기준으로 로그형으로 증가 - 빈번한 단어의 가중치가 너무 높아지는 것을 방지 |
| 증가 빈도 | (하단 참조) | - 최빈 단어를 기준으로 상대적인 빈도 값으로 계산하여 큰 문서에서의 빈도 값이 크게 나타나는 것을 방지할 수 있음 |
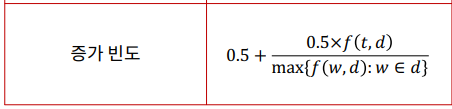
IDF을 알기 전 DF에 대해서 먼저 알아보자
DF: Document Frequency
: 특정 키워드가 등장한 document의 개수
IDF: inverse Document Frequency
: 전체 문서 개수(D)에서 df를 나눈 값
: 사전에 idf를 계산하는데 사용된 문서의 집합 ( 혹은 코퍼스 )에 존재하지 않는 단어에 대해서, IDF를 고려하면 분모가 0이 되기에 이를 방지하기 위해 1을 더한다.
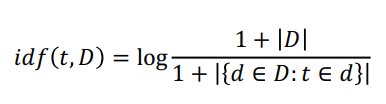
'정리 > Machine Learning' 카테고리의 다른 글
| RoBERTa 리뷰의 리뷰 (0) | 2022.07.07 |
|---|---|
| Transformer (0) | 2022.07.07 |
| [FastCampus The RED 추천시스템] 추천 시스템을 돌릴 때 고려사항 (0) | 2021.11.10 |
| [FastCampus The RED 추천시스템] 추천 시스템 성능평가 (0) | 2021.11.10 |
| [FastCampus The RED 추천시스템] 개요 ~ 추천 시스템 분류 (0) | 2021.11.10 |

model training 순서
- 데이터 로딩
- 데이터 행, 열 확인
- 데이터 그룹핑 및 집계
- 차트
- 데이터 분할
- 평균 값 계산
- RMSE, MAE 계산
- 포스터 이미지 표시
CBF 기반 예측
아이템 유사도 기반 평점 예측
예) 영화 평점 예상 문제
가정: 유사한 영화에는 유사한 평점을 부여할 것이다.

$$ \hat{r}_{u, i} = \frac{\sum _{j \in I_{u}} sim(i, j)*r_{u, j}}{\sum _{j \in I_{u}} sim(i, j)} $$
- r : 사용자 u의 아이템 j에 대한 평점
- I : 사용자 u가 평가한 아이템 집합
- sim(i, j); 두 아이템 i와 j의 유사도
컨텐츠 기반 유사도 측정
sim(i, j)
- 두 아이템 간의 유사도를 어떻게 정량화 할 것이냐가 관건
- CBF에서는 유사도를 정량화 하기 위해서 컨텐츠 자체가 가진 특성을 활용
- 뉴스: 제목, 기사 내용 등
- 영화: 장르, 감독, 출연자, 줄거리 등
- 상품: 카테고리, 가격, 상품 이미지, 상품 설명 등
영화의 장르를 이용해 유사도를 측정

영화를 장르의 집합으로 간주해보면

이 때, 집합 유사도에 대해서 알아보자.
1. Jaccard Similarity
$$ sim(i, j) = J(S_{i}, S_{j}) = \frac{|S_{i}\cap S_{j}|}{|S_{i} \cup S_{j}|} $$
2. Sorensen-Dice Similarity
$$ sim(i, j) = D(S_{i}, S_{j}) = \frac{2|S_{i}\bigcap S_{j}|}{|S_{i}| + |S_{j}|} $$

이 때, 집합으로만 계산하면 복잡한 계산을 하기 힘들어 진다.
유사도를 벡터 공간으로 확대
- 원소에 해당하는 차원을 상정하면 집합은 쉽게 벡터로 표현 가능
- 이진 벡터(Binary Vector)는 집합을 표현할 수 있음
- 각 원소(차원)의 가중치를 달리 적용하는 것이 수월해 짐
벡터 연산 중,
Distance & Similarity
1. Euclidean Distance
$$ d(x, y) = ||x - y||_{2} $$
2. (TODO)Cosine Similarity
$$ sim(x, y) = cos(\theta) = \frac{x^{T}y}{||x||_{2}||y||_{2}} $$
3. Pearson (Correlation) similarity
$$ sim(x, y) = P(x, y) = \frac{\sum_{i=1}^{d}(x_{i} - \bar{x}) \cdot (y_{i} - \bar{y})}{\sqrt{{\sum_{i=1}^{d}(x_{i} - \bar{x})^2}} \sqrt{\sum_{i=1}^{d}(y_{i} - \bar{y})^2}} $$
$$ \bar{x} = \frac{1}{d} \sum_{i=1}^{d} x_{i} $$
$$ \bar{y} = \frac{1}{d} \sum_{i=1}^{d} y_{i} $$
TODO) pearson similarity와 cosine similarity의 관계
BoW - 말뭉치
: 하나의 문서 안에 들어간 단어들의 종류와 수

IF-IDF
tfidf(t, d, D) = tf(t, d) * idf(t, D)
TF : Term Frequence
| 방식 | 계산 식 | 설명 |
| 단순 빈도 | f(t, d) | 문서 내에서의 단어의 출현 횟수로 계산 |
| 불린 빈도(boolean) | 1 if t in d, else 0 | 단어의 출현 여부만을 고려 |
| 로그 스케일 빈도 | log(f(t, d) + 1 ) | - 출현 빈도를 기준으로 로그형으로 증가 - 빈번한 단어의 가중치가 너무 높아지는 것을 방지 |
| 증가 빈도 | (하단 참조) | - 최빈 단어를 기준으로 상대적인 빈도 값으로 계산하여 큰 문서에서의 빈도 값이 크게 나타나는 것을 방지할 수 있음 |
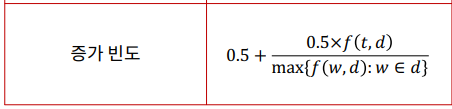
IDF을 알기 전 DF에 대해서 먼저 알아보자
DF: Document Frequency
: 특정 키워드가 등장한 document의 개수
IDF: inverse Document Frequency
: 전체 문서 개수(D)에서 df를 나눈 값
: 사전에 idf를 계산하는데 사용된 문서의 집합 ( 혹은 코퍼스 )에 존재하지 않는 단어에 대해서, IDF를 고려하면 분모가 0이 되기에 이를 방지하기 위해 1을 더한다.
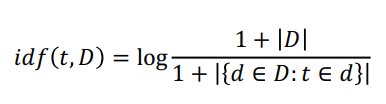
'정리 > Machine Learning' 카테고리의 다른 글
| RoBERTa 리뷰의 리뷰 (0) | 2022.07.07 |
|---|---|
| Transformer (0) | 2022.07.07 |
| [FastCampus The RED 추천시스템] 추천 시스템을 돌릴 때 고려사항 (0) | 2021.11.10 |
| [FastCampus The RED 추천시스템] 추천 시스템 성능평가 (0) | 2021.11.10 |
| [FastCampus The RED 추천시스템] 개요 ~ 추천 시스템 분류 (0) | 2021.11.10 |
