추가 및 수정사항
- 2023.03.22. gradient descent에 대한 오해 추가
오해의 소지가 있는 부분
- 구글링을 하다 보면, SGD, Momentum, Adam 등의 gradient descent methods를 최적화 알고리즘의 종류라고 설명해 놓은 글들을 많이 볼 수 있었다. 물론 일부는 맞는 말이지만, 이런 글은 optimization method가 gradient descent method만 있는 것으로 오해할 수 있을 것 같았다. gradient method, 즉 경사하강법은 최적화 알고리즘 중 하나이며 그 외에도 다른 최적화 알고리즘이 있다는 걸 말해주고 싶다. 내 말을 뒷받침해 줄 자료를 찾다가 다음 페이지를 찾았다.
6. Optimization methods
이제 우리가 생각해야할 것은 Loss function이 나왔을 때, 어떻게 Optimize할 것이냐에 대한 문제입니다. (상세 내용 보충 필요) ##**1) Optimi…
wikidocs.net
wikipedia: https://en.wikipedia.org/wiki/Mathematical_optimization
Mathematical optimization - Wikipedia
From Wikipedia, the free encyclopedia Study of mathematical algorithms for optimization problems Graph of a given by z = f(x, y) = −(x² + y²) + 4. The global maximum at (x, y, z) = (0, 0, 4) is indicated by a blue dot. Nelder-Mead minimum search of Sim
en.wikipedia.org
경사하강법이란
- 경사 하강법은 1차 근삿값 발견용 최적화 알고리즘이다. 즉 최적화 알고리즘 중 하나. 기본 개념은 함수의 기울기를 구하고 경사의 반대 방향으로 계속 이동시켜 극소값에 이를때까지 반복.
경사 하강법을 설명하기 위해서 산이나 계곡을 주로 예시로 든다.
앞이 보이지 않은채 산 한가운데에 떨어져 있다고 가정할 때, 산을 내려가기 위해 할 수 있는 가장 쉬운 방법은 경사를 따라 내려가는 것이다. 그렇게 되면 만약 local minimum에만 빠지지 않는다면 무난하게 산 아래로 내려갈 수 있게 될 것이다.
경사하강법도 마찬가지로 주어진 점에서 기울기를 파악해 경사를 내려가는 방향으로 점을 계속 이동시키면서 극솟값을 찾는 과정이다.
그렇다면 경사 하강법은 왜 쓰일까?
- 비슷하게 미분을 사용하는 방법으로, 미분 값이 0이 되는 지점을 찾아서 해결하면 되지 않을까? 라고 생각해볼 수 있다. 하지만, 머신러닝에 쓰이는 함수는 미분을 통해서 해를 구하기에는 너무 복잡한 수식이어서 계산하기에 너무 오래 걸리고, 계산해야 하는 파라미터가 늘어날 수록 계산하는 더욱 시간이 늘어난다고 한다.
- 따라서 미분 값을 계산하기 보다는 보다는 한걸음씩 반복해서 (
노가다) 밟아가며 극솟값을 찾아가는 것이 컴퓨터 입장에서는 더 간단하고 쉬운 일이라고 한다. - 컴퓨터의 특기는 단순 반복 작업이라는 걸 한 번 더 생각하게 한다.
경사 하강법을 알기 위해서는 미분을 먼저 알아야 한다.
미분에 관해서는 스킵
참고로 python에서 쓰이는 미분 관련 라이브러리는 sympy가 있다.
참고) https://mingchin.tistory.com/174
경사하강법의 과정
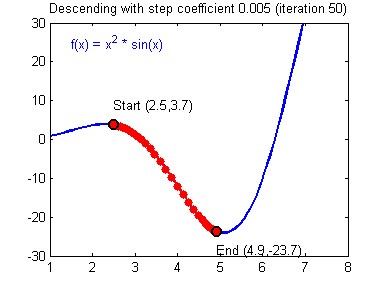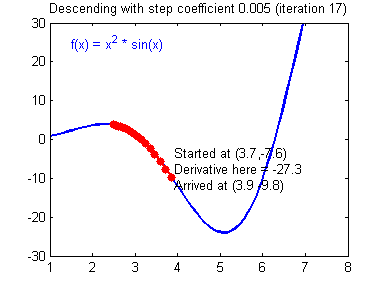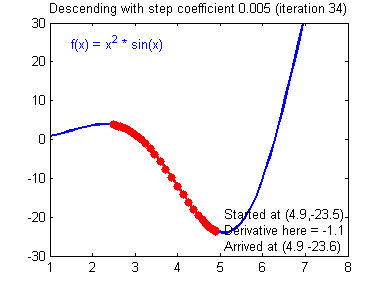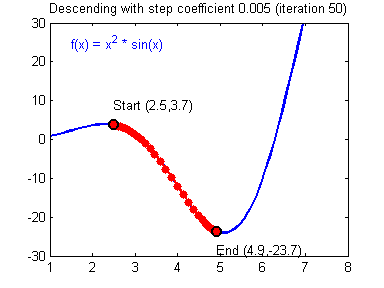
경사하강법의 과정은 다음과 같다.
파라미터를 x, 그래프를 나타내는 함수를 f(x) 라고 하자.
- 현재 파라미터(x)에서의 기울기(f'(x)를 구한다.
- 파라미터에서 기울기에서 학습률을 곱한 값을 빼고, 해당 결과로 파라미터를 업데이트 (x <- x - (λ * f'(x))
- 극솟값을 찾을 때까지 반복
만약 그림처럼 극솟값의 왼쪽에서 시작한다면 미분값은 음수가 나올것이다. 반대로 오른쪽에서 시작한다면 미분값은 양수가 나올 것이다. 예를 들어 x=4에서 f'(x)=-1이라고 하고, x=6에서 f'(x)=1이라고 하자. 학습률은 0.01이라고 하자.
해당 위치에서 경사하강법을 적용하면,
- x=4인 경우
- x <- 4 - (-1) * 0.01, 따라서 x = 4.01
- x=6인 경우,
- x <- 6 - (1) * 0.01, 따라서 x = 5.99
여기서 중요한 점. 미분값이 양수가 나왔던, 음수가 나왔던 경사하강법에서 변수 x를 업데이트 해주기 위해서는 미분값을 빼주면 된다는 것이다.
반대로 말하면, 값을 증가시키고 싶다면(경사상승법) 미분값을 변수에 더해주면 된다.
한계 및 대처
1. 학습률은 사람이 직접 지정해줘야 하는데, 학습률이 너무 작으면 업데이트 되는 크기가 너무 작아 최적값을 찾는데 한세월이 걸리거나 못찾는 경우가 발생할 수 있으며, 너무 크면 값이 튀어버려 마찬가지로 최적값을 못찾을 수 있다.
2. 경사하강법은 그 순간순간의 기울기를 파악해서 입력값에서 기울기를 뺌으로써 내려가는 형태를 띄고 있다. 따라서 그리디 알고리즘 중에 하나라고 할 수 있는데, 경사하강법의 함정은 local minimum에 빠질 수 있다는 것이다.
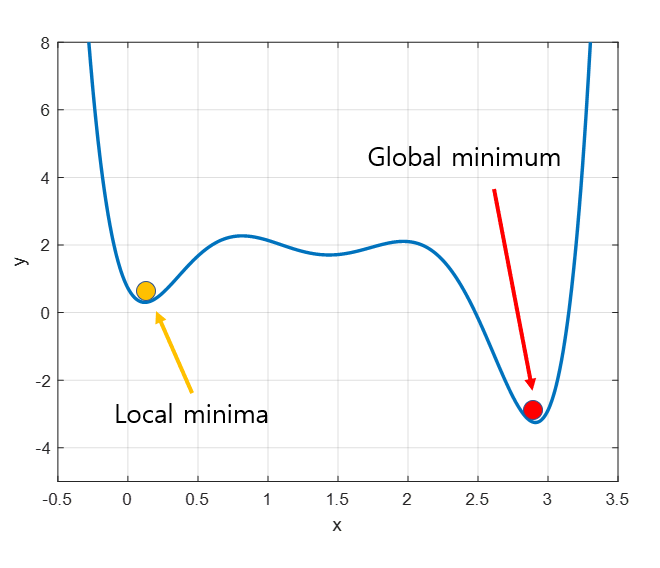
local minimum 및 여러 부작용을 개선하고, 성능을 높이기 위해 다양한 개선사항들이 많이 나왔다.
Adaptive gradient Descent 방법은 학습 도중에 학습률을 업데이트할 수 있고, Momentum을 활용하면 local minimum에 빠지는 함정을 방지할 수도 있다.
그리고 이 두 개념을 합친게 Adam이라는 알고리즘인데, 경사하강법 알고리즘은 다음 포스팅에~
기타. 좋은 읽을거리
https://news.samsungdisplay.com/21209
쉽게 알아보는 공학이야기 15 – 최적화
과학에는 하나의 정답이 존재하지만, 공학에는 다수의 해결 방안이 가능합니다. 여러 가지 해결 방안 중 가장 적합한 것을 찾아가는 과정을 최적화(optimization)라 합니다. 최적화 이론은 최대나
news.samsungdisplay.com
참고)
https://hi-guten-tag.tistory.com/205
[머신러닝 - 이론] 경사 하강법 (Gradient Descent)
1. 경사 하강법의 정의 경사 하강법(傾斜下降法, Gradient descent)은 1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기(경사)를 구하고 경사의 반대 방향으로 계속 이동시켜 극값
hi-guten-tag.tistory.com
https://angeloyeo.github.io/2020/08/16/gradient_descent.html
'정리 > Machine Learning' 카테고리의 다른 글
| [논문 리뷰]cycleGAN - Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks (0) | 2023.04.05 |
|---|---|
| Gradient Descent Methods (0) | 2023.02.18 |
| RoBERTa 리뷰의 리뷰 (0) | 2022.07.07 |
| Transformer (0) | 2022.07.07 |
| [FastCampus The RED 추천시스템] CBF (0) | 2021.11.11 |
