목적
- 한 번에 하나씩의 설명변수(X)를 사용하여 정확한 예측이 가능한 규칙들의 집합 생성
- 최종 결과물은 나무를 뒤집어 놓은 형태인 규칙들의 집합
용어
- 노드.node : 입력 데이터 공간의 특정 영역
- 부모 노드.parent node : 분기 전 노드
- 자식 노드. child node : 부모 노드로부터 분기 후 파생된 노드
- 분기 기준. split criterion: 한 부모 노드를 두 개 이상의 자식 노드들로 분기하는데 사용되는 변수 및 기준 값
- 시작/뿌리 노드. root node: 전체 데이터를 포함하는 노드
- 말단/잎새 노드 leaf node: 더 이상 분기가 수행되지 않는 노드
장점 ( 출처: 위키 백과 )
- 결과를 해석하고 이해하기 쉽다. 간략한 설명만으로 결정 트리를 이해하는 것이 가능하다.
- 자료를 가공할 필요가 거의 없다. 다른 기법들의 경우 자료를 정규화하거나 임의의 변수를 생성하거나 값이 없는 변수를 제거해야 하는 경우가 있다.
- 수치 자료와 범주 자료 모두에 적용할 수 있다. 다른 기법들은 일반적으로 오직 한 종류의 변수를 갖는 데이터 셋을 분석하는 것에 특화되어 있다. (일례로 신경망 학습은 숫자로 표현된 변수만을 다룰 수 있는 것에 반해 관계식(relation rules)은 오직 명목 변수만을 다룰 수 있다.
- 화이트박스 모델을 사용한다. 모델에서 주어진 상황이 관측 가능하다면 불 논리를 이용하여 조건에 대해 쉽게 설명할 수 있다. (결과에 대한 설명을 이해하기 어렵기 때문에 인공신경망은 대표적인 블랙 박스 모델이다.)
- 안정적이다. 해당 모델 추리의 기반이 되는 명제가 다소 손상되었더라도 잘 동작한다.
- 대규모의 데이터 셋에서도 잘 동작한다. 방대한 분량의 데이터를 일반적인 컴퓨터 환경에서 합리적인 시간 안에 분석할 수 있다.
핵심 아이디어
- 재귀적 분기: recursive partitioning
- 특정 영역(parent node)에 속하는 개체들을 하나의 기준 변수 값의 번위에 따라 분기
- 분기에 의해 새로 생성된 child node의 동질성이 최대화 되도록 분기점 선택
- 불순도를 측정하는 기준으로는 범주형 변수에 대해서는 지니계수, 수치형 변수에 대해서는 분산을 이용
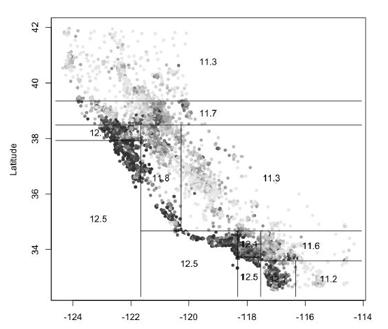
- 입력 변수의 영역을 두 개로 구분 -> 구분하기 전보다 구분된 뒤에 각 영역의 순도(purity, homogeneity)가 증가하도록
- 가지치기
- Over-fitting을 방지하기 위해 하위 노드들을 상위 노드로 결합
- Pre-pruning: Tree를 생성하는 과정에서 최소 분기 기준을 이용하는 사전적 가지치기
- Post-pruning: Full-tree 생성 후, 검증 데이터의 오분류율과 Tree의 복잡도(말단 노드의 수) 등을 고려하는 사후적 가지치기
- 과적합을 방지하기 위해 너무 자세하게 구분된 영역을 통합
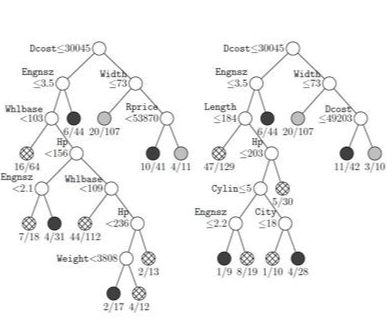
Classification and Regression Tree ( CART )
- 개별 변수의 영역을 반복적으로 분할함으로써 전체 영역에서의 규칙을 생성하는 지도학습 기법
- If_then 형식으로 표현되는 규칙을 생성함으로써, 결과에 대한 예측과 함께 그 이유를 설명할 수 있음
- 수치형 변수와 범주형 변수에 대해 동시 처리 가능
불순도 지표
- 특정한 영역에 개별적인 객체가 얼마나 혼재되어 있는지 알려주는 지표
불순도 지표 1) 지니 계수
- c개의 범주가 존재하는 A영역에 대한 지니 계수
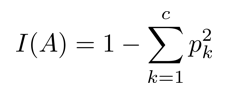
pk: A영역에 속한 객체들 중 k범주에 속하는 레코드의 비율
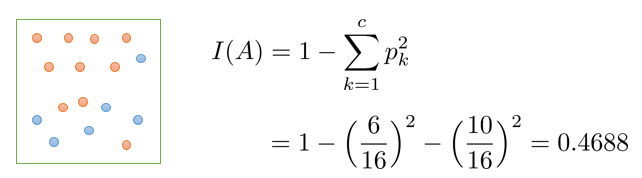
= 1 – (p_blue) – (p_red) = 1 – (6/16)2 – (10/16)2 = 0.4688
- 0 <= I(A) <= 0.5
- 0.5에 가까울수록 순도가 낮다.
두 개 이상 영역에 대한 지니 계수
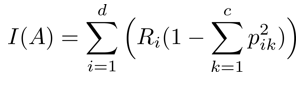
Ri : 분할 전 레코드(전체 레코드) 중 분할 후 i 영역에 속하는 레코드의 비율
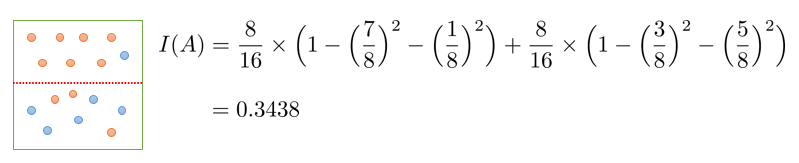
분기 후의 정보 획득 : 0.4688 – 0.3438 = 0.1250
ㄴ 특정 분기 기준의 이득. 얼마나 좋은지를 수치로 표현.
불순도 지표 2: Deviance
특정 영역에 대한 Deviance
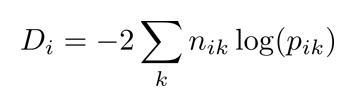
nik – 범주 안에 있는 특정 레코드의 개수
pik – 범주 안에 있는 특정 레코드의 비율
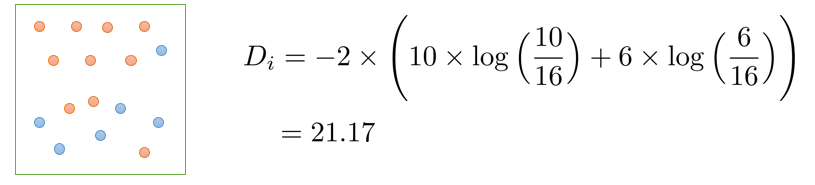
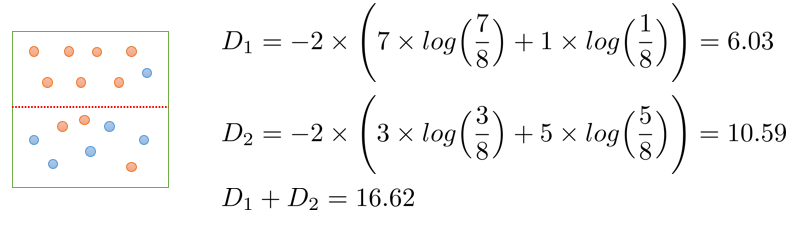
분기 후의 정보 획득(Information gain): 21.17-16.62=4.55
CART Algorithm
- 지니계수( Gini index )를 불순도 지표로 한 알고리즘
- 한 변수를 기준으로 해 정렬
- 변수의 정렬 순서, 정렬 기준(오름차순 / 내림차순)은 최종 모델에 영향을 주지 않음
- 순차적으로 가능한 분기점에 대한 정보 획득 계산
가지치기
- 재귀적 분기는 모든 말단노드의 순도가 100%일 때 종료
- overfitting의 문제가 생기는데, 이 경우에 noise조차 패턴으로 취급할 수 있음
- 따라서 generalization 성능을 향상시켜야 함. ( 새로운 데이터에 대한 예측 성능 저하의 위험을 감소시켜야..)
post-pruning
Full tree를 형성한 뒤 적절한 수준에서 말단 노드를 결합하는 가지치기를 수행
검증 데이터에 대한 오분류율이 증가하는 시점에서 가지치기 수행
full tree에 비해 구조가 단순한 decision tree가 생성됨
비용 복잡도(cost complexity)를 사용하여 최적의 decision tree 구조를 선택
비용 복잡도 ( Cost Complexity )
CC(T) = Err(T) + a*L(T)
- CC(T) = 의사결정나무의 비용 복잡도 (낮을수록 우수한 의사결정나무)
- ERR(T) = 검증데이터에 대한 오분류율
- L(T) = 말단 노드의 수 ( 구조의 복잡도 )
- a = ERR(T)와 L(T)를 결합하는 가중치 ( 사용자에 의해 부여됨, 일반적인 소프트웨어 패키지에서는 default 값이 존재)
사전적 가지치기 ( pre-pruning )
- full-tree 까지 가면서 시간낭비하지 않고, 미리 가지가 자라는 것을 막음
- 제약조건 부여
- 제약조건 예시
- 분기 전후 Information Gain의 최저 기준
- 분기 대상이 되는 노드에 속하는 최소 객체 수
- 의사결정나무가 가질 수 있는 최대 깊이 등
decision tree regression
- split을 한 번 한 회귀모형의 경우에는 하나의 계단처럼 생겼다.
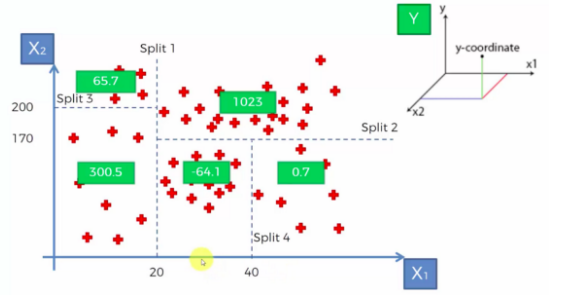
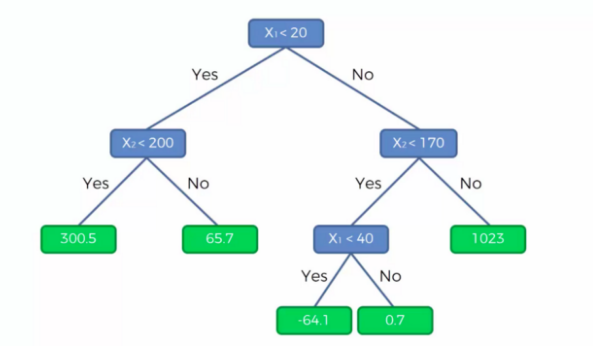
그림을 예로 들어서 보면, 해당 노드(영역)에 속하는 모든 개체의 종속변수(Y) 값의 평균으로 예측한다.
불순도 측정
SSE(sum of squared error) :
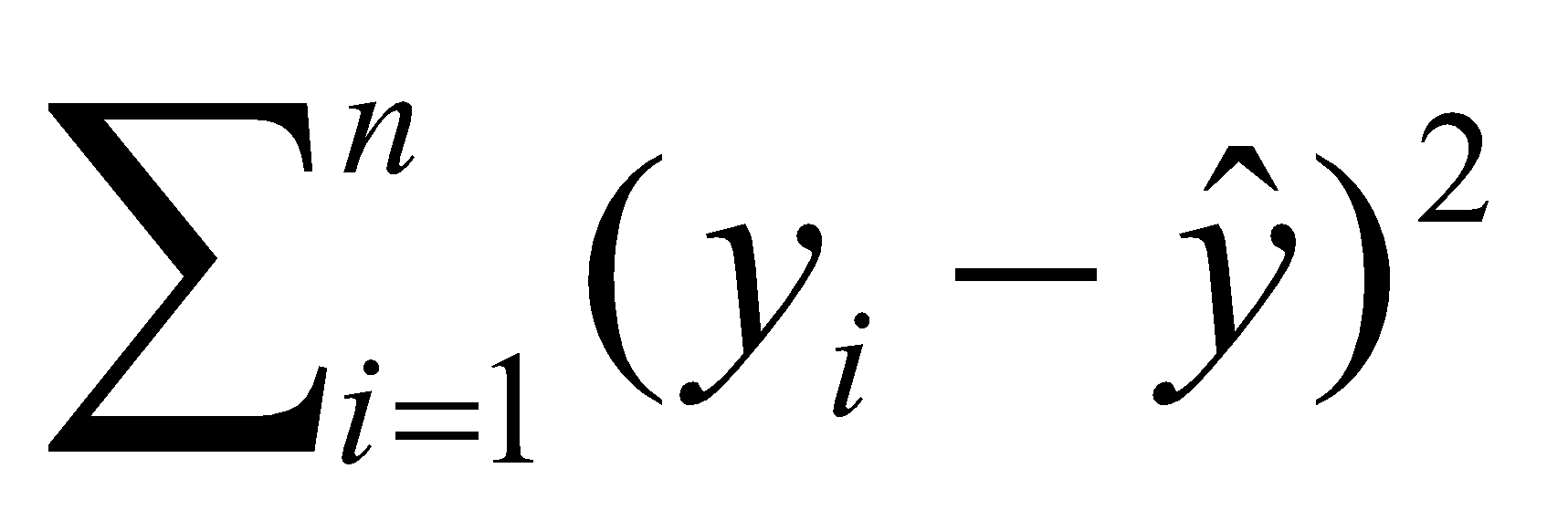
참고)
https://riverzayden.tistory.com/6
'정리 > Machine Learning' 카테고리의 다른 글
| [kaggle - Google Brain - Ventilator Pressure Prediction] 2. data preprocess ~ define architecture ( LSTM ) (0) | 2021.11.08 |
|---|---|
| [kaggle - Google Brain - Ventilator Pressure Prediction] 1. Data load ~ EDA (0) | 2021.11.08 |
| [Deep Learning] Deep Learning 주요 순서 정리 (0) | 2021.11.05 |
| [DL 기본] 210914 수업 내용 정리 (0) | 2021.09.14 |
| [머신러닝] 분류모델 평가지표(Evaluation Metrics for Machine Learning Models) (0) | 2021.08.30 |
목적
- 한 번에 하나씩의 설명변수(X)를 사용하여 정확한 예측이 가능한 규칙들의 집합 생성
- 최종 결과물은 나무를 뒤집어 놓은 형태인 규칙들의 집합
용어
- 노드.node : 입력 데이터 공간의 특정 영역
- 부모 노드.parent node : 분기 전 노드
- 자식 노드. child node : 부모 노드로부터 분기 후 파생된 노드
- 분기 기준. split criterion: 한 부모 노드를 두 개 이상의 자식 노드들로 분기하는데 사용되는 변수 및 기준 값
- 시작/뿌리 노드. root node: 전체 데이터를 포함하는 노드
- 말단/잎새 노드 leaf node: 더 이상 분기가 수행되지 않는 노드
장점 ( 출처: 위키 백과 )
- 결과를 해석하고 이해하기 쉽다. 간략한 설명만으로 결정 트리를 이해하는 것이 가능하다.
- 자료를 가공할 필요가 거의 없다. 다른 기법들의 경우 자료를 정규화하거나 임의의 변수를 생성하거나 값이 없는 변수를 제거해야 하는 경우가 있다.
- 수치 자료와 범주 자료 모두에 적용할 수 있다. 다른 기법들은 일반적으로 오직 한 종류의 변수를 갖는 데이터 셋을 분석하는 것에 특화되어 있다. (일례로 신경망 학습은 숫자로 표현된 변수만을 다룰 수 있는 것에 반해 관계식(relation rules)은 오직 명목 변수만을 다룰 수 있다.
- 화이트박스 모델을 사용한다. 모델에서 주어진 상황이 관측 가능하다면 불 논리를 이용하여 조건에 대해 쉽게 설명할 수 있다. (결과에 대한 설명을 이해하기 어렵기 때문에 인공신경망은 대표적인 블랙 박스 모델이다.)
- 안정적이다. 해당 모델 추리의 기반이 되는 명제가 다소 손상되었더라도 잘 동작한다.
- 대규모의 데이터 셋에서도 잘 동작한다. 방대한 분량의 데이터를 일반적인 컴퓨터 환경에서 합리적인 시간 안에 분석할 수 있다.
핵심 아이디어
- 재귀적 분기: recursive partitioning
- 특정 영역(parent node)에 속하는 개체들을 하나의 기준 변수 값의 번위에 따라 분기
- 분기에 의해 새로 생성된 child node의 동질성이 최대화 되도록 분기점 선택
- 불순도를 측정하는 기준으로는 범주형 변수에 대해서는 지니계수, 수치형 변수에 대해서는 분산을 이용

- 입력 변수의 영역을 두 개로 구분 -> 구분하기 전보다 구분된 뒤에 각 영역의 순도(purity, homogeneity)가 증가하도록
- 가지치기
- Over-fitting을 방지하기 위해 하위 노드들을 상위 노드로 결합
- Pre-pruning: Tree를 생성하는 과정에서 최소 분기 기준을 이용하는 사전적 가지치기
- Post-pruning: Full-tree 생성 후, 검증 데이터의 오분류율과 Tree의 복잡도(말단 노드의 수) 등을 고려하는 사후적 가지치기
- 과적합을 방지하기 위해 너무 자세하게 구분된 영역을 통합

Classification and Regression Tree ( CART )
- 개별 변수의 영역을 반복적으로 분할함으로써 전체 영역에서의 규칙을 생성하는 지도학습 기법
- If_then 형식으로 표현되는 규칙을 생성함으로써, 결과에 대한 예측과 함께 그 이유를 설명할 수 있음
- 수치형 변수와 범주형 변수에 대해 동시 처리 가능
불순도 지표
- 특정한 영역에 개별적인 객체가 얼마나 혼재되어 있는지 알려주는 지표
불순도 지표 1) 지니 계수
- c개의 범주가 존재하는 A영역에 대한 지니 계수
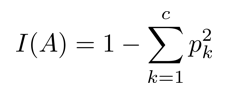
pk: A영역에 속한 객체들 중 k범주에 속하는 레코드의 비율
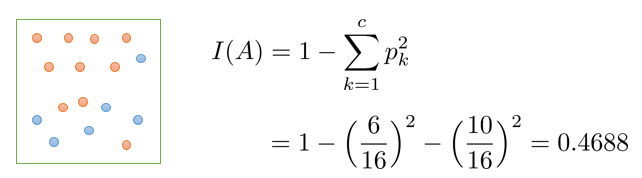
= 1 – (p_blue) – (p_red) = 1 – (6/16)2 – (10/16)2 = 0.4688
- 0 <= I(A) <= 0.5
- 0.5에 가까울수록 순도가 낮다.
두 개 이상 영역에 대한 지니 계수
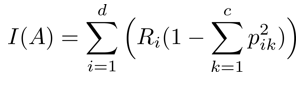
Ri : 분할 전 레코드(전체 레코드) 중 분할 후 i 영역에 속하는 레코드의 비율
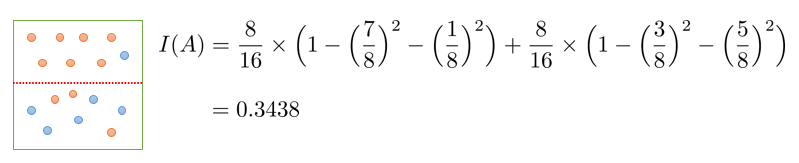
분기 후의 정보 획득 : 0.4688 – 0.3438 = 0.1250
ㄴ 특정 분기 기준의 이득. 얼마나 좋은지를 수치로 표현.
불순도 지표 2: Deviance
특정 영역에 대한 Deviance
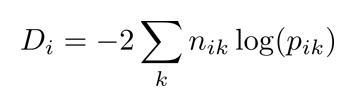
nik – 범주 안에 있는 특정 레코드의 개수
pik – 범주 안에 있는 특정 레코드의 비율
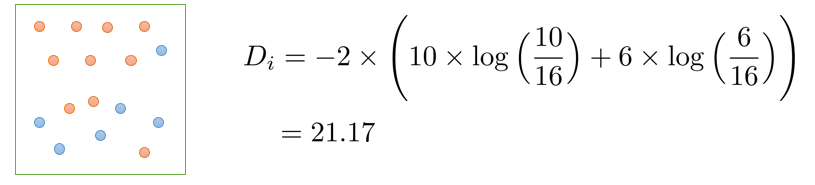
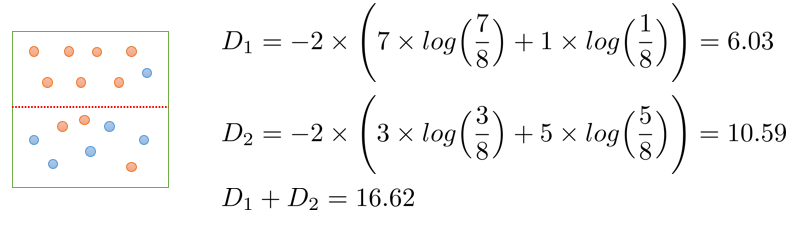
분기 후의 정보 획득(Information gain): 21.17-16.62=4.55
CART Algorithm
- 지니계수( Gini index )를 불순도 지표로 한 알고리즘
- 한 변수를 기준으로 해 정렬
- 변수의 정렬 순서, 정렬 기준(오름차순 / 내림차순)은 최종 모델에 영향을 주지 않음
- 순차적으로 가능한 분기점에 대한 정보 획득 계산
가지치기
- 재귀적 분기는 모든 말단노드의 순도가 100%일 때 종료
- overfitting의 문제가 생기는데, 이 경우에 noise조차 패턴으로 취급할 수 있음
- 따라서 generalization 성능을 향상시켜야 함. ( 새로운 데이터에 대한 예측 성능 저하의 위험을 감소시켜야..)
post-pruning
Full tree를 형성한 뒤 적절한 수준에서 말단 노드를 결합하는 가지치기를 수행
검증 데이터에 대한 오분류율이 증가하는 시점에서 가지치기 수행
full tree에 비해 구조가 단순한 decision tree가 생성됨
비용 복잡도(cost complexity)를 사용하여 최적의 decision tree 구조를 선택
비용 복잡도 ( Cost Complexity )
CC(T) = Err(T) + a*L(T)
- CC(T) = 의사결정나무의 비용 복잡도 (낮을수록 우수한 의사결정나무)
- ERR(T) = 검증데이터에 대한 오분류율
- L(T) = 말단 노드의 수 ( 구조의 복잡도 )
- a = ERR(T)와 L(T)를 결합하는 가중치 ( 사용자에 의해 부여됨, 일반적인 소프트웨어 패키지에서는 default 값이 존재)
사전적 가지치기 ( pre-pruning )
- full-tree 까지 가면서 시간낭비하지 않고, 미리 가지가 자라는 것을 막음
- 제약조건 부여
- 제약조건 예시
- 분기 전후 Information Gain의 최저 기준
- 분기 대상이 되는 노드에 속하는 최소 객체 수
- 의사결정나무가 가질 수 있는 최대 깊이 등
decision tree regression
- split을 한 번 한 회귀모형의 경우에는 하나의 계단처럼 생겼다.


그림을 예로 들어서 보면, 해당 노드(영역)에 속하는 모든 개체의 종속변수(Y) 값의 평균으로 예측한다.
불순도 측정
SSE(sum of squared error) :
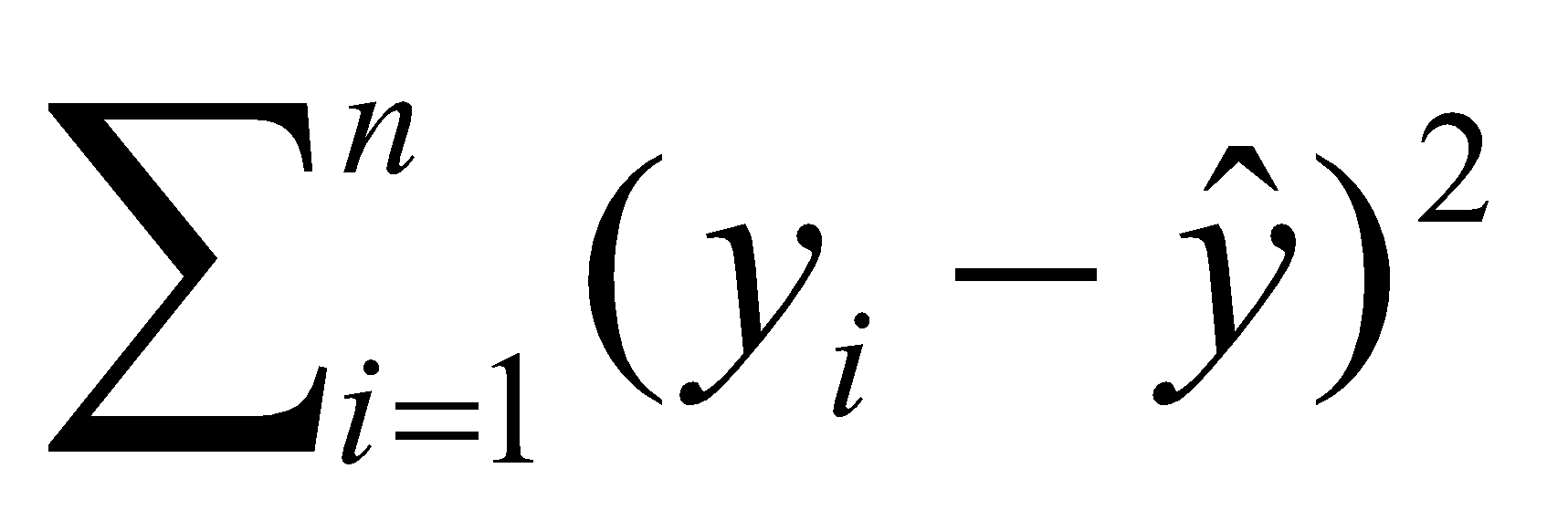
참고)
https://riverzayden.tistory.com/6
'정리 > Machine Learning' 카테고리의 다른 글
| [kaggle - Google Brain - Ventilator Pressure Prediction] 2. data preprocess ~ define architecture ( LSTM ) (0) | 2021.11.08 |
|---|---|
| [kaggle - Google Brain - Ventilator Pressure Prediction] 1. Data load ~ EDA (0) | 2021.11.08 |
| [Deep Learning] Deep Learning 주요 순서 정리 (0) | 2021.11.05 |
| [DL 기본] 210914 수업 내용 정리 (0) | 2021.09.14 |
| [머신러닝] 분류모델 평가지표(Evaluation Metrics for Machine Learning Models) (0) | 2021.08.30 |
