확률과 가능도(우도)
확률
: 주어진 분포에서 특정 사건이 관측될 확률
확률 = P(관측값 X | 확률분포 D)
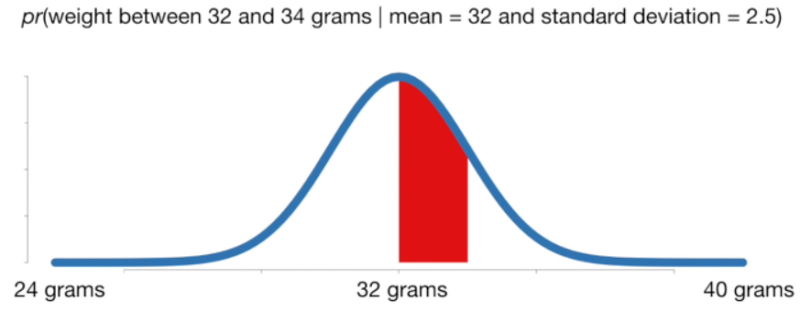
가능도
: 주어진 값이 특정 확률분포에서 관측될지에 대한 확률
가능도 = L(확률분포 D | 관측값 X)
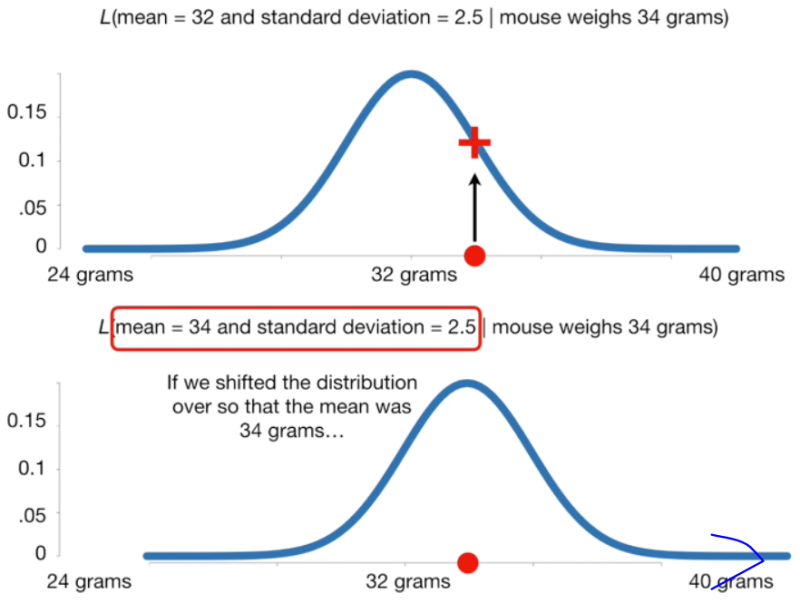
최대 우도 추정( Maximum Likelihood)
: 주어진 관측값에 대한 총 가능도(모든 가능도의 곱)가 최대가 되게 하는 분포를 찾는 것.
여러 개의 관측값을 구했을 때, 이렇게 관측 될 가능성이 가장 큰 확률분포를 구하는 것이 MLE이다.
먼저 이 포스팅에서는 두 가지 가정을 한다.
- 가정1. 관측값이 이렇게 분포되었다고 가정

- 가정2. 관측값에 대한 분포는 정규분포를 띈다고 가정
정규분포의 식을 구할 때는 두 가지만 구하면 된다.
- 평균 μ
- 표준편차 σ
step 1. 평균 구하기
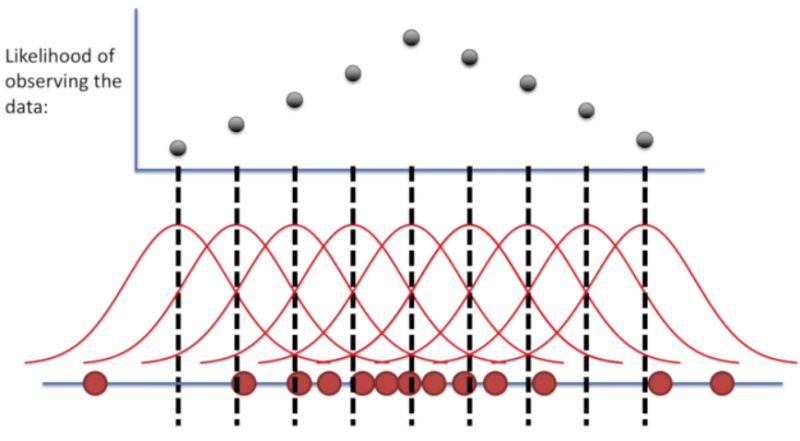
임의의 표준편차에서 평균을 바꾸면 위 사진과 같이 나올 것이다.
이 때 likehood가 최대가 되는 지점일 때 평균을 구한다.
step 2. 표준편차 구하기
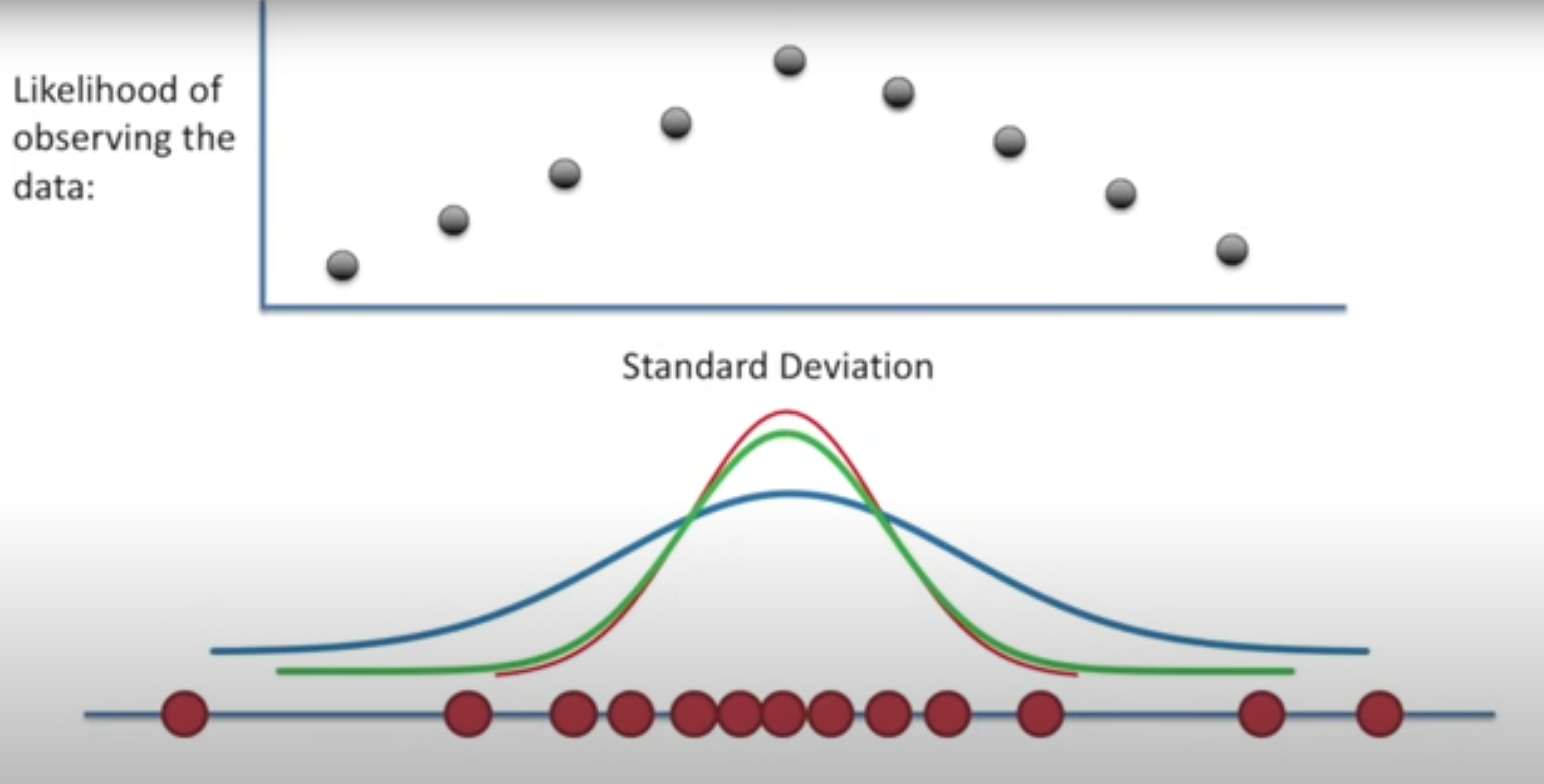
마찬가지로 평균을 고정시킨 상태에서 표준편차를 바꾸면 위 사진과 같이 나올 것이며, likelihood가 가장 클 때의 표준편차를 구하면
N(μ, σ^2)인 분포가 나오게 된다.
Likelihood function
앞서 말했듯이, likelihood는 주어진 데이터가 어떤 분포로부터 나왔을 확률 또는 가능성을 의미한다.
수치적으로 이 가능도를 계산하기 위해, 각 데이터 샘플에서 후보 분포에 대한 높이(즉 likelihood 기여도)를 계산해서 다 곱한 것을 이용할 수 있다.
계산된 높이를 곱해주는 것의 이유는 모든 데이터들의 추출이 독립적으로 연달아 일어나는 사건이기 때문이라고 한다.
따라서 likelihood를 수학적으로 표현하면 다음과 같다.
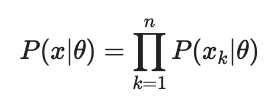
여기서 x는 데이터 값이고, Θ가 분포를 의미한다고 생각하면 될 것 같다.
결론적으로 MLE는 위의 Likelihood function의 최대값을 찾는 방법이라고 할 수 있다.
이 때, log 함수는 단조증가 함수이기 때문에 log를 취한 함수가 최대가 되는 값을 찾으나 그냥 likelihood function의 최대가 되는 값을 찾으나 정의역의 함수 입력값은 동일하므로, 계산의 편의를 위해 보통 likelihood function은 여기에 log를 취해서 덧셈으로 만들어주는, log-likelihood function을 이용한다.
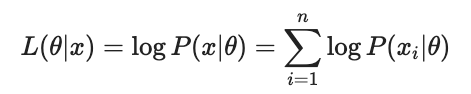
함수의 최대값을 찾는 방법 중 가장 일반적인 방법은 미분을 활용하는 것. 따라서 Θ에 대해서 편미분하고 그 값이 0이 되도록 하는 Θ를 찾으면, likelihood function을 최대화 시키는 Θ를 찾을 수 있다.
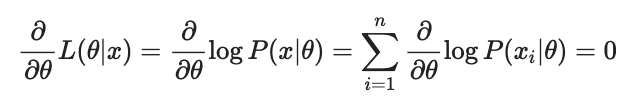
참고자료)
블로그
https://jjangjjong.tistory.com/41
statquest
Probability is not Likelihood. Find out why!!!
Maximum Likelihood, clearly explained!!!
공돌이의 수학정리노트
'정리' 카테고리의 다른 글
| [python] shallow copy vs deep copy (0) | 2024.03.04 |
|---|---|
| mutable vs immutable object (0) | 2024.03.04 |
| Bayse's rule(베이즈 정리) (0) | 2023.04.13 |
| [colab+spark] colab에서 spark 쓰는법 (0) | 2021.12.01 |
| [DataScience 기초](정리 필요) group-k fold (0) | 2021.10.27 |
확률과 가능도(우도)
확률
: 주어진 분포에서 특정 사건이 관측될 확률
확률 = P(관측값 X | 확률분포 D)

가능도
: 주어진 값이 특정 확률분포에서 관측될지에 대한 확률
가능도 = L(확률분포 D | 관측값 X)

최대 우도 추정( Maximum Likelihood)
: 주어진 관측값에 대한 총 가능도(모든 가능도의 곱)가 최대가 되게 하는 분포를 찾는 것.
여러 개의 관측값을 구했을 때, 이렇게 관측 될 가능성이 가장 큰 확률분포를 구하는 것이 MLE이다.
먼저 이 포스팅에서는 두 가지 가정을 한다.
- 가정1. 관측값이 이렇게 분포되었다고 가정

- 가정2. 관측값에 대한 분포는 정규분포를 띈다고 가정
정규분포의 식을 구할 때는 두 가지만 구하면 된다.
- 평균 μ
- 표준편차 σ
step 1. 평균 구하기

임의의 표준편차에서 평균을 바꾸면 위 사진과 같이 나올 것이다.
이 때 likehood가 최대가 되는 지점일 때 평균을 구한다.
step 2. 표준편차 구하기

마찬가지로 평균을 고정시킨 상태에서 표준편차를 바꾸면 위 사진과 같이 나올 것이며, likelihood가 가장 클 때의 표준편차를 구하면
N(μ, σ^2)인 분포가 나오게 된다.
Likelihood function
앞서 말했듯이, likelihood는 주어진 데이터가 어떤 분포로부터 나왔을 확률 또는 가능성을 의미한다.
수치적으로 이 가능도를 계산하기 위해, 각 데이터 샘플에서 후보 분포에 대한 높이(즉 likelihood 기여도)를 계산해서 다 곱한 것을 이용할 수 있다.
계산된 높이를 곱해주는 것의 이유는 모든 데이터들의 추출이 독립적으로 연달아 일어나는 사건이기 때문이라고 한다.
따라서 likelihood를 수학적으로 표현하면 다음과 같다.
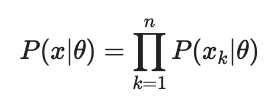
여기서 x는 데이터 값이고, Θ가 분포를 의미한다고 생각하면 될 것 같다.
결론적으로 MLE는 위의 Likelihood function의 최대값을 찾는 방법이라고 할 수 있다.
이 때, log 함수는 단조증가 함수이기 때문에 log를 취한 함수가 최대가 되는 값을 찾으나 그냥 likelihood function의 최대가 되는 값을 찾으나 정의역의 함수 입력값은 동일하므로, 계산의 편의를 위해 보통 likelihood function은 여기에 log를 취해서 덧셈으로 만들어주는, log-likelihood function을 이용한다.
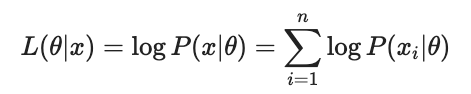
함수의 최대값을 찾는 방법 중 가장 일반적인 방법은 미분을 활용하는 것. 따라서 Θ에 대해서 편미분하고 그 값이 0이 되도록 하는 Θ를 찾으면, likelihood function을 최대화 시키는 Θ를 찾을 수 있다.
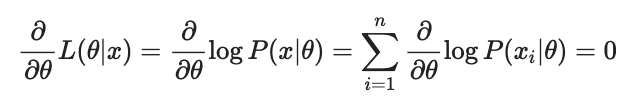
참고자료)
블로그
https://jjangjjong.tistory.com/41
statquest
Probability is not Likelihood. Find out why!!!
Maximum Likelihood, clearly explained!!!
공돌이의 수학정리노트
'정리' 카테고리의 다른 글
| [python] shallow copy vs deep copy (0) | 2024.03.04 |
|---|---|
| mutable vs immutable object (0) | 2024.03.04 |
| Bayse's rule(베이즈 정리) (0) | 2023.04.13 |
| [colab+spark] colab에서 spark 쓰는법 (0) | 2021.12.01 |
| [DataScience 기초](정리 필요) group-k fold (0) | 2021.10.27 |
